Algoritma Support Vector Regression (SVR): Jenis SVM untuk Regresi
Bagi yang berkecimpung di Machine Learning atau Data Science mungkin cukup familiar dengan istilah SVM atau Support Vector Machine.
SVM merupakan salah satu algoritma yang paling populer dan banyak digunakan untuk menangani masalah klasifikasi dalam machine learning. Namun, penggunaan SVM untuk tugas regresi belum banyak dibahas secara luas. Algoritma regresi pada SVM mengakui adanya non-linearitas dalam data dan menyediakan model prediksi yang mumpuni.
Algoritma regresi SVM yang dimaksud adalah Support Vector Regression atau SVR. Support Vector Regression seperti namanya adalah algoritma regresi yang mendukung regresi linier dan non-linier.
Tetapi, sebelum kita masuk ke topik Support Vector Regression (SVR), ada baiknya Anda mengerti terlebih dahulu konsep SVM yang menjadi dasar mengapa SVR dikembangkan. Penjelasan lengkap mengenai SVM sudah dibahas di artikel sebelumnya dan dapat dibaca pada tautan ini.
Baiklah, langsung saja kita masuk ke inti materi mengenai algoritma SVR.
Pengertian Algoritma Support Vector Regression (SVR)
Support Vector Regression (SVR) adalah algoritma supervised learning yang digunakan untuk memprediksi nilai variabel kontinu. SVR menggunakan prinsip yang sama dengan SVM.
Tujuan dasar dari algoritma SVR adalah menemukan garis keputusan yang paling sesuai. Dalam SVR, garis yang paling cocok adalah hyperplane yang memiliki jumlah poin maksimum.
Tidak seperti model regresi lain yang mencoba meminimalkan kesalahan antara nilai aktual dan nilai prediksi, SVR mencoba menyesuaikan garis terbaik dalam nilai ambang batas (jarak antara hyperplane dan boundary line).
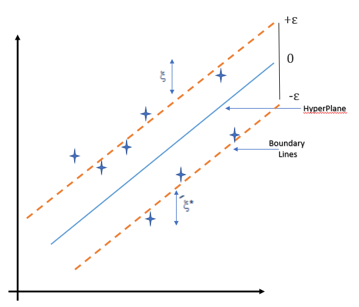
Singkatnya, SVR bekerja untuk mencari nilai terbaik dalam margin tertentu yang disebut epsilon. Perhatikan gambar di bawah ini untuk memahami SVR:
 |
| Sumber: educba.com |
Untuk memahami gambar di atas kita perlu untuk mengetahui istilah berikut:
- Hyperplane. Hyperplane adalah garis pemisah antara dua kelas data dalam dimensi yang lebih tinggi dari dimensi sebenarnya. Dalam SVR, hyperplane didefinisikan sebagai garis yang membantu dalam memprediksi nilai target (kontinu). Titik-titik data di kedua sisi hyperplane yang paling dekat dengan hyperplane disebut Support Vector.
- Kernel. Kernel adalah kumpulan fungsi matematika yang mengambil data sebagai input dan mengubahnya menjadi bentuk yang diperlukan.
- Fungsi kernel. Fungsi kernel umumnya digunakan untuk menemukan hyperplane di ruang dimensi yang lebih tinggi. Jenis kernel yang biasa digunakan dalam SVR adalah kernel sigmoid, kernel polinomial, kernel gaussian, dll.
- Boundary line Boundary line atau garis batas adalah dua garis yang ditarik di sekitar hyperplane pada jarak tertentu (epsilon). Biasanya digunakan untuk membuat margin antara titik data.
Cara Kerja Support Vector Regression
Seperti yang diketahui bahwa SVR bertujuan untuk menangani masalah-masalah terkait regresi. SVR bekerja berdasarkan prinsip SVM dengan sedikit perbedaan.
Apabila diberikan titik-titik data, algoritma SVR mencoba menemukan kurva. Karena SVR adalah algoritma regresi, maka alih-alih menggunakan kurva sebagai batas keputusan, SVR menggunakan kurva untuk menemukan kecocokan antara vektor dan posisi kurva.
Support Vector membantu dalam menentukan kecocokan terdekat antara titik data dan fungsi yang digunakan untuk merepresentasikannya.
 |
| Sumber: analyticsvidhya.com |
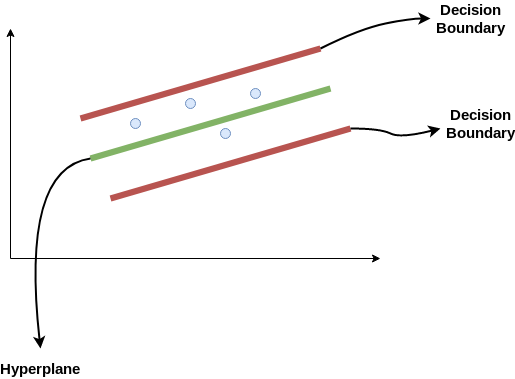
Sebagai contoh, dua garis merah pada gambar di atas dapat dianggap sebagai decision boundary atau batas keputusan sedangkan garis hijau sebagai hyperplane.
Hal pertama yang perlu dipahami yakni decision boundary. Pertama, kita coba tarik garis pada jarak berapapun, misal ‘e’ dari hyperplane. Sehingga, garis yang kita gambar ada pada jarak ‘+e’ dan ‘-e’ dari hyperplane. ‘e’ disebut sebagai epsilon.
 |
| Sumber: medium.com |
Dengan asumsi bahwa persamaan pada hyperplane sebagai berikut:
dimana:
y = nilai perkiraan
w = weight
x = variabel penjelas
b = bias
Maka untuk persamaan decision boundary menjadi:
Jadi, setiap hyperplane yang memenuhi SVR harus memenuhi persamaan:
Dengan demikian, kita dapat mengatakan bahwa model SVR mencoba memenuhi kondisi -e < y-wx+b < e yang mana titik yang dekat pada hyperplane atau support vector berada dalam garis batasan (boundary).
Oleh karena itu, model SVR akan mengambil titik-titik yang berada dalam decision boundary dan memiliki tingkat kesalahan (error) paling kecil, atau berada dalam batas toleransi.
SVR linear
Untuk SVR linear dapat dirumuskan sebagai berikut:
SVR non-linear
Untuk SVR non-linear diperlukan fungsi kernel. Fungsi kernel mengubah data menjadi ruang fitur berdimensi lebih tinggi untuk memungkinkan dilakukannya pemisahan secara linier.
Fungsi kernel yang bisa digunakan:
1. Polinomial
2. Gaussian Radial Basis Function (RBF)
Kelebihan Support Vector Regression
Meskipun SVR jarang digunakan, namun memiliki kelebihan tertentu seperti:
- Model keputusan dapat dengan mudah diperbarui.
- Dapat menggunakan beberapa classifier yang dilatih pada berbagai jenis data menggunakan aturan probabilitas.
- SVR melakukan komputasi yang lebih rendah dibandingkan dengan teknik regresi lainnya.
- Memiliki kemampuan generalisasi yang sangat baik, dengan akurasi prediksi yang tinggi.
- Implementasi SVR cenderung mudah
Kekurangan Support Vector Regression
Beberapa kelemahan yang dimiliki oleh SVR saat menangani masalah regresi adalah sebagai berikut:
- Penggunaannya tidak cocok untuk kumpulan data yang besar.
- Jika jumlah fitur untuk setiap titik data melebihi jumlah sampel data pelatihan, SVR berperforma buruk.
- Model keputusan tidak berkinerja sangat baik ketika kumpulan data memiliki lebih banyak noise yaitu kelas target tumpang tindih.
Penutup
Demikianlah penjelasan singkat mengenai algoritma Support Vector Regression (SVR). Semoga informasi di atas dapat bermanfaat dan membantu Anda memahami lebih dalam mengenai cara kerja beserta kelebihan dan kekurangan algoritma SVR.
Jika Anda tertarik dengan artikel serupa Anda dapat mengunjungi rubrik Machine Learning atau membaca artikel lainnya mengenai Algoritma Apriori.
Salam!
Referensi:



Posting Komentar untuk "Algoritma Support Vector Regression (SVR): Jenis SVM untuk Regresi"
Komentar SPAM akan disensor. Harap gunakan kalimat yang tidak menjurus pada SARA dan pornografi.